18.1 Midpoint Rule

In the midpoint rule you approximate the area under the curve as a rectangle with the height as the function value at the midpoint of the interval:

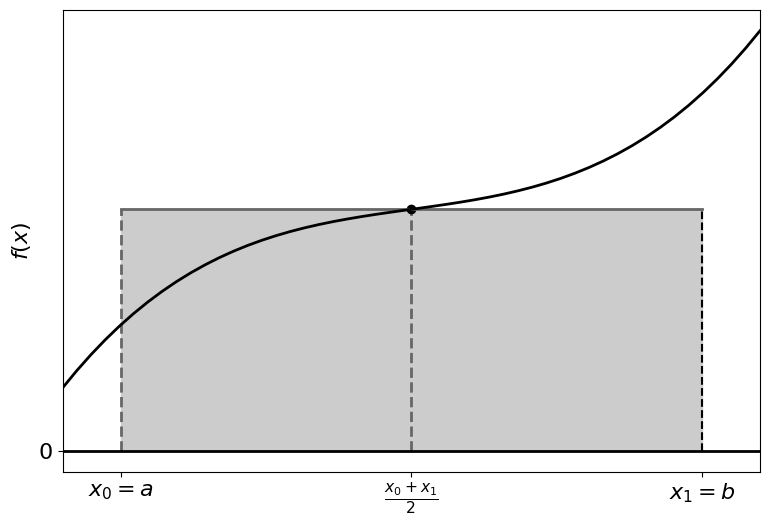
\[ \int_a^b f(x)~ dx \approx f\left(\frac{a + b}{2}\right) (b - a) \]

Composite Midpoint Rule

For a more accurate solution we can subdivide the interval further, constructing rectangles for each subinterval, with the function value of the midpoint used as the height:

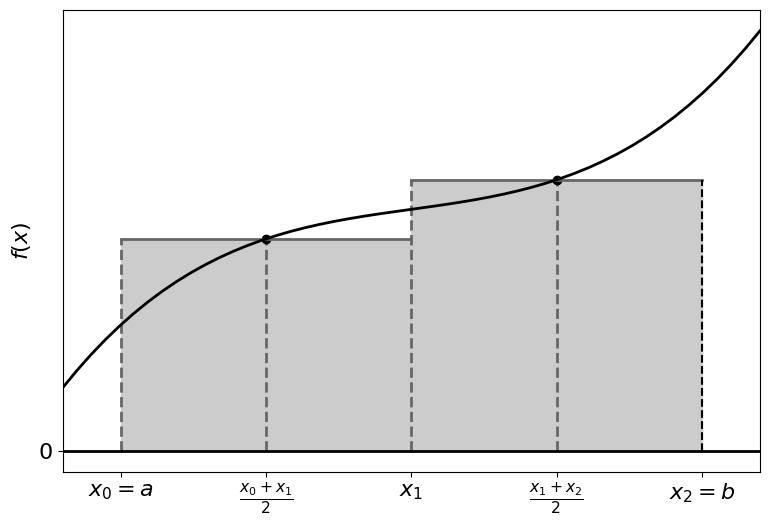
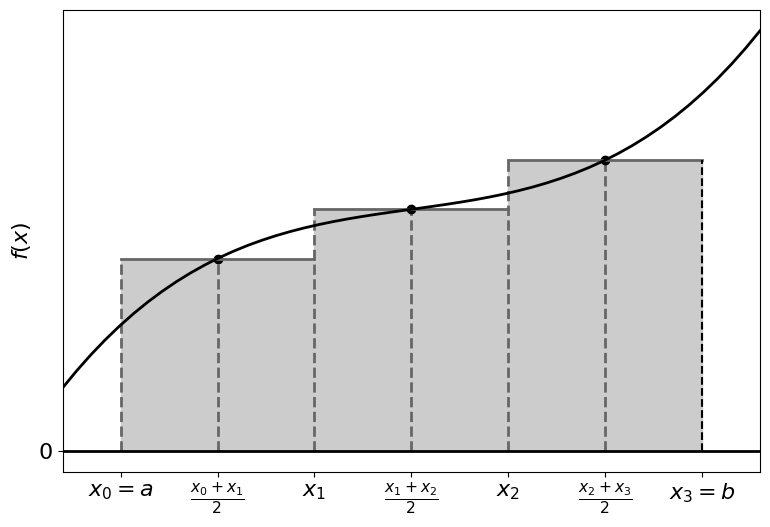
For \(n\) subdivisions:

\[ \int_a^b f(x)~ dx \approx \sum_{i=1}^n (x_i - x_{i-1}) f\left(\frac{x_i + x_{i-1}}{2}\right) \]

If these divisions are equal, then

\[ x_i - x_{i-1} = \frac{b - a}{n} \]

which makes the approximation:

\[ \int_a^b f(x) ~dx \approx \frac{b - a}{n} \sum_{i=1}^n f\left(\frac{x_i + x_{i-1}}{2}\right) \]

Assuming that \(n\) is chosen so that \(0 < \tfrac{b - a}{n} < 1\), the (global) error for this method is \(O\left(\tfrac{1}{n}^2\right)\) [IntMid1].

References

[IntMid1]

James F. Epperson. An Introduction to Numerical Methods and Analysis. John Wiley & Sons, Inc., Hoboken, New Jersey, second edition edition, 2013.