Exercise 12.3

Question 1

Consider a conical spiral defined by:

\[\begin{align*} x &= s \cos(s \pi)\\ y &= s \sin(s \pi)\\ z &= s \end{align*}\]

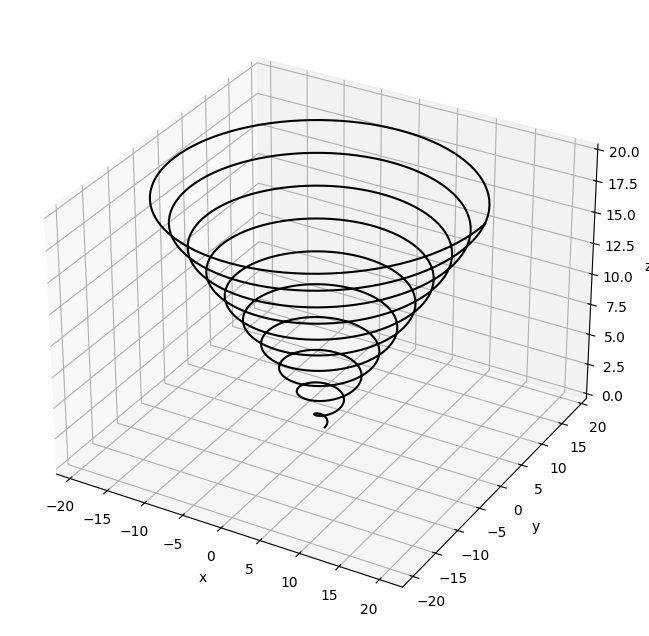
Write a script to plot this spiral as a curve in 3D space, starting with a value for \(s = 0\). What value of \(s\) do you need to end on to make the spiral wind around 10 times, as in the figure above?

Question 2

The simplest example of a 2D Gaussian can be defined by:

\[ f(x, y) = A \exp\left( -\left(\frac{\left(x - x_0\right)^2}{2 \sigma_x^2} + \frac{\left(y - y_0\right)^2}{2 \sigma_y^2} \right) \right) \]

where \(A\) is the height of the Gaussian, \(\exp()\) is the exponential function \(e^{()}\), \((x_0, y_0)\) is the position of the peak of the Gaussian, and \(\sigma_x\) and \(\sigma_y\) determine the spread of the Gaussian along the \(x\) and \(y\) axis respectively.

Plot a surface defined by:

\[ z = f(x, y) \]

For a Gaussian with

• \(A = 1\)

• \(x_0 = y_0 = 0\)

• \(\sigma_x = 1\)

• \(\sigma_y = 2\)

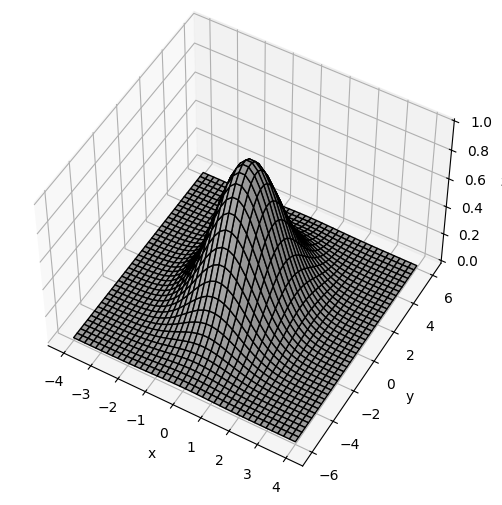
as illustrated below (you need not match the illustration):

Hint: for the \(\exp\) you can use the numpy.exp() function.

Bonus: Apply a colormap to the surface using the \(z\)-value to determine the color value.

Question 3

Plot the whole surface of a sphere of radius 1 centered on the origin.

Though it’s possible to use a single surface, you may want to try breaking the sphere up into 2 hemispheres. See if you can figure out how to use a single surface later.

Hint: If you want to set the aspect ratio of the axes to be equal, set_aspect() isn’t going to help for the Axis3D. Instead we have to manually set the axis limits so that the ratio matches the value of get_box_aspect. Let’s outline this for the limits containing the sphere, note that this will be slightly more complex if the limits are not symmetrical.

#The limits should AT LEAST contain the sphere
min_limit = 1

aspect = ax.get_box_aspect()

#Scaling the aspect so that the minimum value matches min_limit
limits = aspect / aspect.min() * min_limit

#Setting the limits
ax.set_xlim(-limits[0], limits[0])
ax.set_ylim(-limits[1], limits[1])
ax.set_zlim(-limits[2], limits[2])