Recursive Functions¶
Recursive functions are functions that make calls to themselves.
They can be used in place of loops. Though in Python they don’t necessarily provide a more efficient solution, there are many problems for which a recursive function is the most elegant and convenient solution.
Worked Example
One of the most famous implementations of a recursive function is to implement the factorial:
This is achieved by using the recurrence relation:
The recursive function which solves this is:
def factorial(n):
if not type(n) is int:
print('n must be an integer')
return
if n <0:
print('n must be greater than or equal to 0')
return
if n == 0:
return 1
return n*factorial(n-1)
Note, an important aspect of this function is the return value of 1 for n == 0. This is called the base class, without it the function would never finish it’s recursion.
Putting this function into action:
factorial(-1)
n must be greater than or equal to 0
factorial(0.5)
n must be an integer
factorial(0)
1
factorial(1)
1
factorial(5)
120
factorial(10)
3628800
The inner workings of this factorial() function are fairly subtle. The (informal) flow diagram below illustrates the function call for factorial(5):
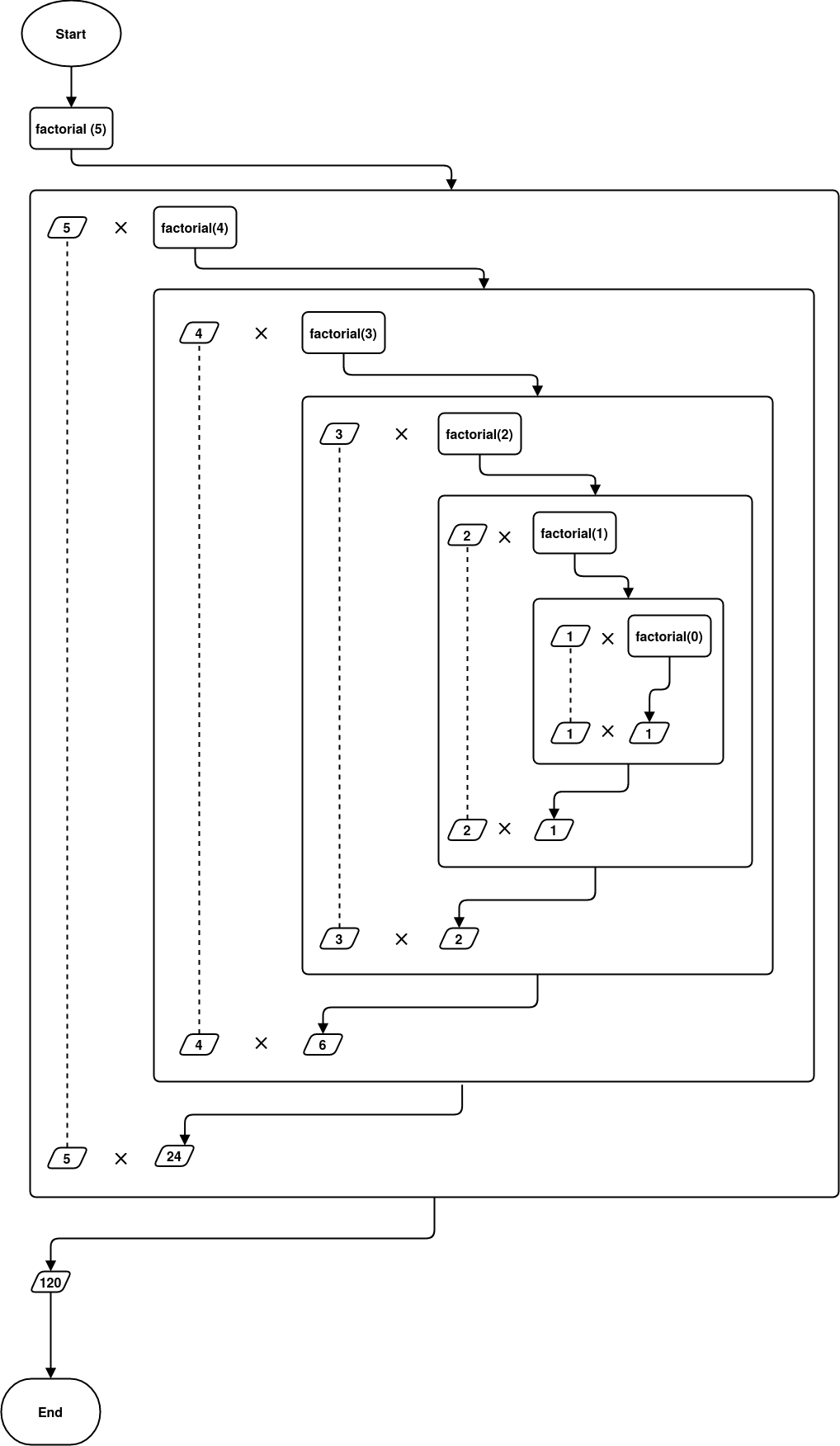
The Base Class¶
As mentioned earlier, a recursive function must have at least one base class. The base class is a return state that doesn’t make another recursive function call.
It’s also important to make sure that the recursion eventually reaches the base class when designing your function.
