Contents

Newton-Raphson Method

The Newton-Raphson method is similar to the secant method, except here we construct a straight line that passes through a point \((x_0, f(x_0))\) with a gradient of \(f^\prime (x_0)\), the tangent of \(f(x)\) at that point. The next point, \(x_1\), is the intersection of this line with the \(x\)-axis:

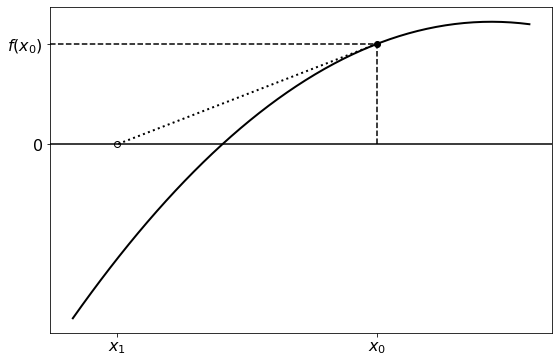
../../../_images/newton_4_0.png

As before, this process can be repeated with \(x_1\), and the rest of the points after it, converging closer to the root. Further iterations are illustrated in the following figures:

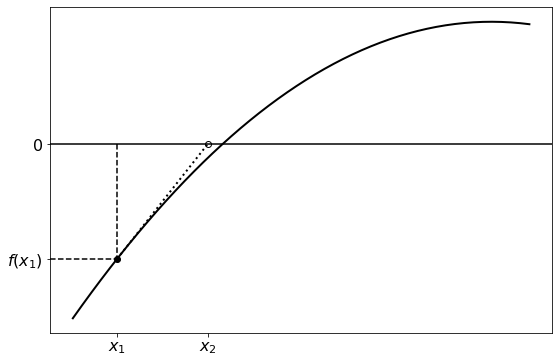
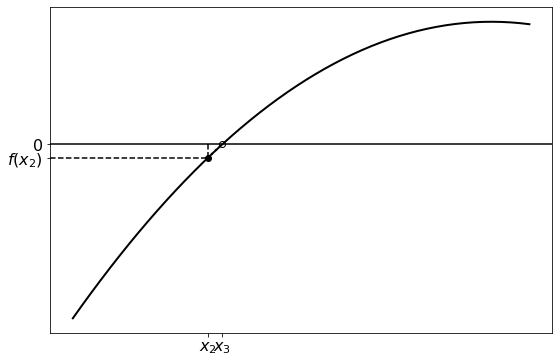
../../../_images/newton_6_0.png ../../../_images/newton_6_1.png

To calculate the point \(x_n\) using the previous point \(x_{n-1}\), we start by constructing the line running through \((x_{n-1}, f(x_{n-1}))\):

\[ \frac{y - f(x_{n-1})}{x - x_{n-1}} = f^\prime (x_{n-1}) \]

at the \(x\)-intercept, \(y = 0\) and \(x = x_n\):

\[\begin{split} \begin{align*} \frac{0 - f(x_{n-1})}{x_n - x_{n-1}} &= f^\prime(x_{n-1})\\ \therefore x_n &= x_{n-1} - \frac{f(x_{n-1})}{f^\prime(x_{n-1})}\\ \end{align*} \end{split}\]

Precision

Similarly to the secant method, the precision for the Newton-Raphson method can be set for a given tolerance by finding \(n\) such that:

\[ |x_n - x_{n-1}| < \text{tolerance} \]

Instability

The Newton-Raphson method suffers from much the same issues as the secant method.

Secant Method Comparing the Methods